The charge-to-mass ratio (![]() ) of an electron is a fundamental property of this subatomic particle that relates its electric charge (
) of an electron is a fundamental property of this subatomic particle that relates its electric charge (![]() ) to its mass (
) to its mass (![]() ). It is one of the key parameters that characterize the behavior of electrons in electric and magnetic fields, playing a pivotal role in physics, chemistry, and material science. The discovery and measurement of the charge-to-mass ratio were instrumental in identifying the electron as a distinct particle and understanding its properties.
). It is one of the key parameters that characterize the behavior of electrons in electric and magnetic fields, playing a pivotal role in physics, chemistry, and material science. The discovery and measurement of the charge-to-mass ratio were instrumental in identifying the electron as a distinct particle and understanding its properties.

This article explores the concept of the charge-to-mass ratio of an electron, its historical discovery, the mathematical derivation of the formula, and its significance in modern science, supported by examples to illustrate its applications.
What is the Charge-to-Mass Ratio of an Electron?
The charge-to-mass ratio (![]() ) is defined as the electric charge of an electron divided by its mass. It is a measure of how strongly the electron is influenced by electric and magnetic fields relative to its mass. Mathematically, it is expressed as:
) is defined as the electric charge of an electron divided by its mass. It is a measure of how strongly the electron is influenced by electric and magnetic fields relative to its mass. Mathematically, it is expressed as:
![]()
where:
 = charge of the electron (
= charge of the electron (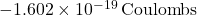 ),
),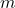 = mass of the electron (
= mass of the electron (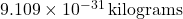 ).
).
For an electron, the charge-to-mass ratio has a value of approximately:
![]()
This ratio indicates that the electron’s charge is relatively large compared to its extremely small mass, making it highly responsive to electromagnetic forces.
Historical Context: J.J. Thomson’s Experiment
The discovery and measurement of the charge-to-mass ratio of the electron are attributed to J.J. Thomson in 1897. Thomson’s experiment was groundbreaking in the identification of the electron as a fundamental particle. Using a cathode ray tube, Thomson demonstrated that cathode rays were composed of negatively charged particles (later named electrons) and measured their charge-to-mass ratio.
Thomson’s Experiment Setup
Thomson used a cathode ray tube with the following components:
1. Electrodes: Cathode rays (streams of electrons) were emitted from the cathode and accelerated toward the anode.
2. Electric Field: Parallel plates created an electric field to deflect the electrons.
3. Magnetic Field: A magnetic field perpendicular to the electric field was used to counteract the deflection caused by the electric field.
4. Fluorescent Screen: The deflection of the cathode rays was observed on a fluorescent screen.
By adjusting the strengths of the electric and magnetic fields, Thomson was able to balance the forces acting on the electrons and determine their charge-to-mass ratio.
Key Observations and Results
Thomson’s experiment revealed:
1. Deflection in Electric and Magnetic Fields: Cathode rays were deflected by electric and magnetic fields, confirming that they carried charge.
2. Independence from Material: The charge-to-mass ratio of the particles was the same regardless of the gas in the tube or the electrode material, proving that electrons were a universal particle.
From his measurements, Thomson calculated the charge-to-mass ratio of the electron to be:
![]()
This value closely matches the modern accepted value, demonstrating the accuracy of his experiment.
Derivation of the Charge-to-Mass Ratio Formula
The charge-to-mass ratio is derived by analyzing the motion of an electron in combined electric and magnetic fields. The key principles are based on Newton’s laws of motion and the Lorentz force law.
1. Motion in an Electric Field
When an electron moves through an electric field (![]() ), it experiences an electric force given by:
), it experiences an electric force given by:
![]()
where:
 = force due to the electric field,
= force due to the electric field, = charge of the electron,
= charge of the electron,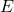 = electric field strength.
= electric field strength.
This force accelerates the electron, causing it to deviate from its path.
2. Motion in a Magnetic Field
When the electron moves through a magnetic field (![]() ), it experiences a magnetic force given by:
), it experiences a magnetic force given by:
![]()
where:
 = velocity of the electron,
= velocity of the electron,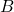 = magnetic field strength.
= magnetic field strength.
This force is perpendicular to both the velocity and the magnetic field direction, causing the electron to follow a circular trajectory if no other forces are present.
3. Balancing Electric and Magnetic Forces
In Thomson’s experiment, the electric and magnetic fields were adjusted so that their forces balanced each other, preventing the electron from being deflected. This balance is described as:
![]()
Canceling ![]() (since the charge is the same for both forces):
(since the charge is the same for both forces):
![]()
From this, the velocity (![]() ) of the electron can be expressed as:
) of the electron can be expressed as:
![]()
4. Circular Motion in a Magnetic Field
When the magnetic force acts alone, the electron moves in a circular path due to the centripetal force. The magnetic force provides the centripetal force:
![]()
where:
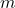 = mass of the electron,
= mass of the electron, = radius of the circular path.
= radius of the circular path.
Rearranging to solve for ![]() :
:
![]()
Substituting ![]() into the equation:
into the equation:
![]()
This final formula allows the charge-to-mass ratio (![]() ) to be determined experimentally using measurable quantities: the electric field (
) to be determined experimentally using measurable quantities: the electric field (![]() ), magnetic field (
), magnetic field (![]() ), and the radius of the electron’s circular path (
), and the radius of the electron’s circular path (![]() ).
).
Applications of the Charge-to-Mass Ratio of the Electron
The charge-to-mass ratio of the electron is a fundamental quantity with wide-ranging applications in physics, technology, and scientific research.
1. Understanding Subatomic Particles
The charge-to-mass ratio is a cornerstone in identifying and studying subatomic particles. By comparing the ![]() values of particles, scientists can distinguish between electrons, protons, and other charged particles.
values of particles, scientists can distinguish between electrons, protons, and other charged particles.
Example: The proton’s charge-to-mass ratio is much smaller than the electron’s due to its significantly higher mass, even though both have charges of the same magnitude.
2. Design of Cathode Ray Tubes (CRTs)
The principles of the charge-to-mass ratio are fundamental in the operation of cathode ray tubes, which were used in older television sets, oscilloscopes, and early computer monitors.
Example: In CRTs, electrons are accelerated and deflected by electric and magnetic fields to create images on a fluorescent screen. The charge-to-mass ratio helps calculate the electron trajectories for precise image rendering.
3. Particle Accelerators
In particle accelerators, such as cyclotrons and synchrotrons, the charge-to-mass ratio is used to calculate the behavior of charged particles in magnetic and electric fields. This information allows scientists to control and accelerate particles to high speeds for experiments.
Example: The Large Hadron Collider (LHC) uses principles of ![]() to direct and focus charged particles like protons and electrons in high-energy collisions.
to direct and focus charged particles like protons and electrons in high-energy collisions.
4. Mass Spectrometry
Mass spectrometry relies on the charge-to-mass ratio to identify and analyze ions in a sample. Ions are accelerated and subjected to magnetic fields, where their trajectories depend on their ![]() values. This technique is widely used in chemistry, biology, and materials science.
values. This technique is widely used in chemistry, biology, and materials science.
Example: In proteomics, mass spectrometry is used to determine the masses of peptides and proteins by analyzing their charge-to-mass ratios, providing insights into their structures.
5. Magnetic Resonance Imaging (MRI)
Although MRI primarily focuses on nuclei, the charge-to-mass ratio of charged particles plays a role in understanding magnetic interactions at the atomic level.
Example: The principles of ![]() help in studying electron orbitals and magnetic properties that influence MRI contrast mechanisms.
help in studying electron orbitals and magnetic properties that influence MRI contrast mechanisms.
6. Space Science and Astronomy
The charge-to-mass ratio of electrons is critical in understanding the behavior of charged particles in space, such as solar wind and cosmic rays. It helps in modeling the interaction of these particles with planetary magnetic fields.
Example: Studying the Earth’s magnetosphere involves analyzing how electrons and other charged particles move under the influence of the planet’s magnetic field.
Example Calculation of 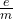
Suppose an electron moves in a circular path with a radius of ![]() in a magnetic field of
in a magnetic field of ![]() and an electric field of
and an electric field of ![]() . To calculate
. To calculate ![]() , use:
, use:
![]()
![]()
This matches the accepted value for ![]() , confirming the calculation.
, confirming the calculation.
Conclusion
The charge-to-mass ratio of an electron (![]() ) is a fundamental property that reveals important insights into the nature of electrons and their behavior in electric and magnetic fields. From J.J. Thomson’s pioneering experiment to modern applications in mass spectrometry, particle accelerators, and space science, this ratio has had a profound impact on our understanding of atomic and subatomic particles. The concept continues to be a cornerstone in both theoretical and applied physics, highlighting the elegance and utility of fundamental measurements in science.
) is a fundamental property that reveals important insights into the nature of electrons and their behavior in electric and magnetic fields. From J.J. Thomson’s pioneering experiment to modern applications in mass spectrometry, particle accelerators, and space science, this ratio has had a profound impact on our understanding of atomic and subatomic particles. The concept continues to be a cornerstone in both theoretical and applied physics, highlighting the elegance and utility of fundamental measurements in science.