Understanding the Identity Function: Definition, Properties, and Examples

In mathematics, the concept of functions is foundational, and among the most fundamental of these is the identity function. The identity function, as its name suggests, returns its input exactly as it is. This function serves as a cornerstone in various mathematical disciplines, including algebra, calculus, and linear algebra. Its simplicity belies its importance, as it plays a significant role in understanding function compositions, transformations, and mappings.

In this article, we will explore the identity function in detail, define its properties, discuss its applications, and provide examples to illustrate its concept and usefulness.

What Is the Identity Function?

An identity function is a function that returns the input value as the output without any changes. In other words, the identity function maps every element in a set to itself. It is generally represented by $f(x) = x$ for all values of $x$ within its domain.

The formal definition of the identity function on a set $X$ is:

$f: X \to X \quad \text{such that} \quad f(x) = x \quad \text{for all } x \in X.$

In this definition:

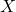$X$ is the domain and range of the function $f$ .
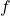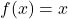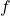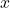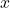$f(x) = x$ indicates that the output of $f$ for any input $x$ is $x$ itself.

The identity function is often denoted by $I_X$ or simply $I$ when the set $X$ is clear from the context. Its output is identical to its input, and this is what gives the identity function its name.

Example of an Identity Function

Consider the function $f(x) = x$ defined on the set of real numbers $\mathbb{R}$ . For any real number input $x$ , the function returns $x$ . So, if we input 5, the function returns 5, and if we input -3, it returns -3.

$f(5) = 5, \quad f(-3) = -3, \quad f(0) = 0$

The function $f(x) = x$ is an identity function because it maps each element to itself.

Properties of the Identity Function

The identity function has several key properties that make it useful in various mathematical applications:

1. Linearity

The identity function is linear. For any two real numbers $a$ and $b$ , and for any values of $x$ and $y$ in the domain of $f$ :

$f(ax + by) = ax + by = a \cdot f(x) + b \cdot f(y)$

This property is why the identity function is considered a linear transformation in the context of linear algebra.

2. Compositional Neutrality

The identity function is a “neutral” element in function composition. When an identity function is composed with any other function $g$ , it leaves $g$ unchanged. Mathematically, for any function $g: X \to X$ :

$f \circ g = g \quad \text{and} \quad g \circ f = g$

where $f$ is the identity function. This property makes the identity function similar to the number 1 in multiplication, as multiplying any number by 1 leaves the number unchanged.

3. Graph of the Identity Function

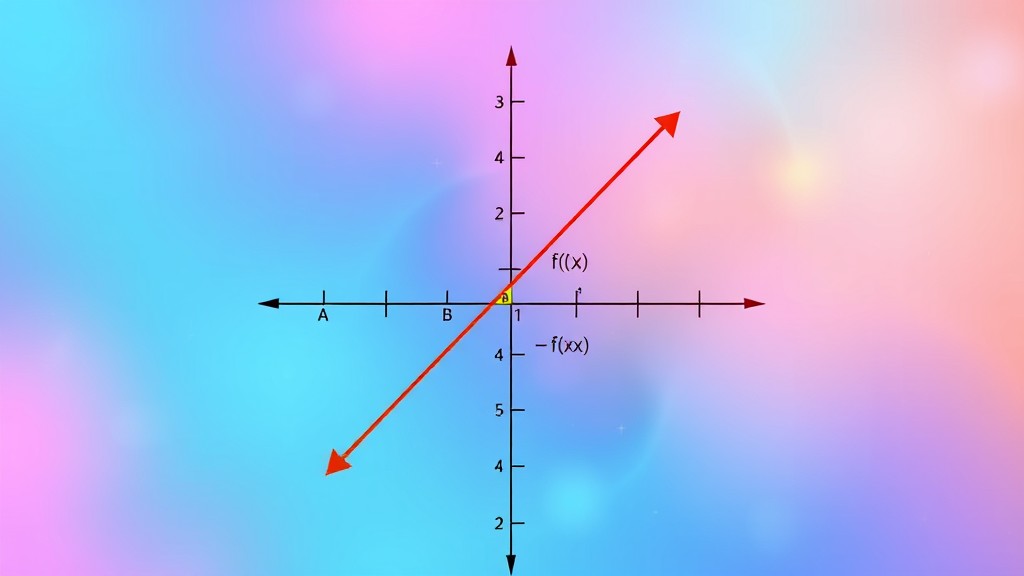
The graph of the identity function $f(x) = x$ on the Cartesian plane is a straight line passing through the origin with a slope of 1. This line has an equation $y = x$ , meaning every point on the graph has coordinates $(x, x)$ .

Example: Plotting the points $(1,1)$ , $(2,2)$ , $(3,3)$ , and $(-1,-1)$ shows that they all lie on the line $y = x$ , demonstrating the identity function’s graph.

4. Invertibility

The identity function is its own inverse. For any $x$ in the domain of $f$ :

$f^{-1}(x) = x$

This property holds because applying the identity function twice returns the original input: $f(f(x)) = x$ .

5. Fixed Points

In an identity function, every point is a fixed point. A fixed point of a function is a point where $f(x) = x$ . In the case of the identity function, this holds for all $x$ in the domain, making every element of the domain a fixed point.

Example: If $f(x) = x$ , then for any $x$ (e.g., 2 or -4), $f(x) = x$ , so each input is a fixed point.

Applications of the Identity Function

The identity function’s simplicity makes it highly versatile in various branches of mathematics and applied fields. Here are a few areas where the identity function is useful:

1. Function Composition and Transformations

In function composition, the identity function serves as a neutral element. It allows transformations without altering the other function’s behavior. This property is useful in functional analysis, where transformations or mappings are composed to study system behaviors.

Example: If $g(x) = x^2$ , composing $g$ with the identity function $I(x) = x$ results in $g(I(x)) = g(x) = x^2$ and $I(g(x)) = g(x) = x^2$ , showing that the identity function leaves $g$ unchanged.

2. Linear Algebra and Matrices

In linear algebra, the identity function corresponds to the identity matrix, which has 1s along the diagonal and 0s elsewhere. When multiplied by any vector or matrix, the identity matrix leaves the vector or matrix unchanged, serving a similar role to the identity function in composition.

Example: For a 2×2 identity matrix $I$ :

$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

Multiplying any vector $v = \begin{bmatrix} a \\ b \end{bmatrix}$ by $I$ gives:

$I \cdot v = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix} = v$

3. Identity in Complex Numbers

In complex numbers, the identity function corresponds to multiplication by 1. The function $f(z) = z$ for any complex number $z$ maps each complex number to itself, preserving both magnitude and phase.

4. Computational Applications

In programming and computational functions, the identity function is often used as a placeholder or default function. It serves as a test function or is used when no transformation is needed, but a function is required to satisfy syntax or structure.

Example: In some programming languages, an identity function might be defined as:
“`python
def identity(x):
return x
“`
This function simply returns the input value, which can be useful in code that requires a default function.

5. Probability and Statistics

In probability, the identity function can represent a variable that does not change under a given transformation. For instance, if a random variable $X$ is transformed by the identity function $f(x) = x$ , its distribution remains unchanged. This is useful in theoretical models and simulations where variables need to be standardized or unchanged.

Examples Illustrating the Identity Function

Example 1: Identity Function in Algebra

Consider a function $f(x) = x$ and a quadratic function $g(x) = x^2 + 3x + 2$ . Composing $g$ with $f$ on both sides gives:

$f(g(x)) = g(x) = x^2 + 3x + 2$

$g(f(x)) = g(x) = x^2 + 3x + 2$

This result shows that composing any function with the identity function leaves the function itself unchanged.

Example 2: Identity Function as a Mapping

Suppose we have a set $S = \{1, 2, 3\}$ and define the identity function $f: S \to S$ such that $f(x) = x$ for each element in $S$ . For each element in $S$ :

$f(1) = 1, \quad f(2) = 2, \quad f(3) = 3$

This mapping demonstrates that the identity function maps each element to itself, preserving the elements in the set without any transformation.

Example 3: Identity Function in Geometry

In geometry, the identity function can represent a transformation that leaves a figure unchanged. For instance, applying the identity transformation to a shape on a plane means the shape remains in the exact same position and orientation.

If a point $(x, y)$ is mapped under the identity function, it remains at $(x, y)$ , indicating that the identity function is equivalent to no movement or transformation at all.

Example 4: Identity Function in Functional Analysis

In functional analysis, the identity function can serve as a test function in iterative calculations. For instance, a system might apply $f(x) = x$ as the initial approximation in algorithms for solving equations, gradually moving to more complex transformations as needed.

Conclusion

The identity function, defined by $f(x) = x$ , is a fundamental mathematical concept that plays an essential role across various areas, including algebra, geometry, linear algebra, and programming. Its properties—such as being linear, compositional neutrality, having fixed points, and being its own inverse—make it unique among functions. The identity function’s simplicity and versatility allow it to serve as a neutral element in compositions, a standard in transformations, and a helpful tool in computational and theoretical contexts. Its applications demonstrate its practical significance, highlighting the importance of even the simplest functions in mathematics and beyond.