An LCR circuit is an electrical circuit consisting of three essential components: an inductor (L), a capacitor (C), and a resistor (R) connected in series or parallel. The LCR circuit is a cornerstone in electronics and electrical engineering, as it helps analyze and control the behavior of alternating current (AC) circuits. This type of circuit is widely used in tuning, filtering, oscillation, and signal processing applications.

In this article, we will delve into the fundamental principles of LCR circuits, their behavior in AC systems, resonance phenomena, and real-world applications, supplemented by examples to illustrate each concept.
—
Components of an LCR Circuit
1. Inductor (L)
- An inductor stores energy in its magnetic field when current flows through it.
- It opposes changes in current due to its inductance (
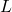 ).
). - The opposition to current is quantified as inductive reactance (
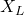 ):
):
![]()
Where:
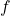 is the frequency of the AC signal.
is the frequency of the AC signal.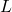 is the inductance in henries (H).
is the inductance in henries (H).
Example: An inductor of ![]() in a circuit with
in a circuit with ![]() has an inductive reactance:
has an inductive reactance:
![]()
—
2. Capacitor (C)
- A capacitor stores energy in its electric field when charged.
- It opposes changes in voltage by allowing current to flow while charging or discharging.
- The opposition to AC current is quantified as capacitive reactance (
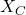 ):
):
![]()
Where:
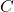 is the capacitance in farads (F).
is the capacitance in farads (F).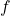 is the frequency of the AC signal.
is the frequency of the AC signal.
Example: A capacitor of ![]() in a circuit with
in a circuit with ![]() has a capacitive reactance:
has a capacitive reactance:
![]()
—
3. Resistor (R)
- A resistor opposes the flow of current, converting electrical energy into heat.
- The opposition is quantified as resistance (
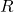 ), measured in ohms (
), measured in ohms (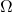 ).
). - Unlike
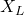 or
or 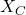 , the resistance is independent of frequency.
, the resistance is independent of frequency.
Example: A ![]() resistor always provides
resistor always provides ![]() resistance regardless of the AC frequency.
resistance regardless of the AC frequency.
—
Types of LCR Circuits
1. Series LCR Circuit
In a series LCR circuit, the inductor, capacitor, and resistor are connected end-to-end, forming a single path for current. The total impedance (![]() ) of the circuit is the vector sum of resistance, inductive reactance, and capacitive reactance:
) of the circuit is the vector sum of resistance, inductive reactance, and capacitive reactance:
![]()
The current through all components is the same, but the voltage across each component differs due to their individual reactances.
—
2. Parallel LCR Circuit
In a parallel LCR circuit, the inductor, capacitor, and resistor are connected across the same two terminals. The total admittance (![]() ) is the sum of the admittances of each branch:
) is the sum of the admittances of each branch:
![]()
Where:
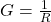 is the conductance.
is the conductance. is the inductive susceptance.
is the inductive susceptance.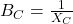 is the capacitive susceptance.
is the capacitive susceptance.
The voltage across each component is the same, but the current through each component depends on its impedance.
—
Behavior of LCR Circuits in AC Systems
The behavior of an LCR circuit depends on the frequency of the AC source, leading to three main conditions:
1. Resonance
Resonance occurs when the inductive reactance equals the capacitive reactance (![]() ):
):
![]()
Where ![]() is the resonant frequency:
is the resonant frequency:
![]()
At resonance:
- The impedance (
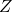 ) of a series LCR circuit is minimum (
) of a series LCR circuit is minimum (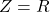 ).
). - The current is maximum in a series LCR circuit.
- Voltage across the inductor and capacitor can be large, though they cancel each other out in the circuit.
Example: For an LCR circuit with ![]() and
and ![]() :
:
![]()
—
2. Below Resonance (Inductive Behavior)
When the frequency is lower than the resonant frequency (![]() ): –
): – ![]() , and the circuit behaves like a capacitive circuit.
, and the circuit behaves like a capacitive circuit.
- Current leads the voltage (phase angle is negative).
—
3. Above Resonance (Capacitive Behavior)
When the frequency is higher than the resonant frequency (![]() ):
):
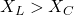 , and the circuit behaves like an inductive circuit.
, and the circuit behaves like an inductive circuit.- Voltage leads the current (phase angle is positive).
—
Power in LCR Circuits
Power in an AC circuit depends on the phase difference (![]() ) between the voltage and current. The average power (
) between the voltage and current. The average power (![]() ) is given by:
) is given by:
![]()
Where:
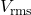 and
and 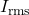 are the root-mean-square values of voltage and current.
are the root-mean-square values of voltage and current.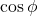 is the power factor, determined by the ratio of resistance to impedance:
is the power factor, determined by the ratio of resistance to impedance:
![]()
Example: For a series LCR circuit with ![]() ,
, ![]() , and
, and ![]() :
:
![]()
The power factor is:
![]()
—
Real-World Applications of LCR Circuits
1. Tuning Circuits
LCR circuits are used in radio receivers to select desired frequencies by adjusting the resonant frequency.
Example: In an AM radio, adjusting the capacitor in an LCR circuit allows it to tune to different stations.
—
2. Filter Circuits
LCR circuits act as filters, blocking or allowing specific frequency ranges:
- Low-Pass Filter: Allows low frequencies to pass while blocking high frequencies.
- High-Pass Filter: Allows high frequencies to pass while blocking low frequencies.
Example: Audio crossover circuits use LCR filters to direct low frequencies to subwoofers and high frequencies to tweeters.
—
3. Oscillators
LCR circuits are used in oscillators to generate stable AC signals at specific frequencies, such as in clocks and communication systems.
Example: A quartz oscillator in a wristwatch relies on an LCR circuit to maintain precise timekeeping.
—
4. Power Factor Correction
LCR circuits are used to improve the power factor in AC power systems, reducing energy losses in transmission.
Example: Industrial systems use capacitors in LCR circuits to balance inductive loads from motors.
—
Practical Considerations
1. Component Tolerances: Variations in ![]() ,
, ![]() , or
, or ![]() can shift the resonant frequency or impedance.
can shift the resonant frequency or impedance.
2. Damping: The resistor dissipates energy, affecting the sharpness of resonance.
3. Quality Factor (![]() ): Measures the sharpness of resonance:
): Measures the sharpness of resonance:
![]()
Where ![]() is the bandwidth.
is the bandwidth.
—
Conclusion
An LCR circuit is a versatile and fundamental component in electronics, capable of filtering, tuning, oscillating, and managing power. By understanding the interplay of inductance, capacitance, and resistance, we can analyze and design systems that harness the principles of resonance and impedance. Whether in radios, power systems, or signal processors, the LCR circuit’s ability to control AC behavior makes it an indispensable tool in modern technology.