Conductivity is a fundamental property in materials science, physics, and electrical engineering, describing a material’s ability to conduct electric current. It quantifies how well a substance allows the flow of charge when subjected to an electric field. Conductivity is critical in analyzing and optimizing materials for electronics, water treatment, and industrial applications.

In this article, we’ll explore the principles of conductivity, its mathematical representation, units, and real-world applications. Examples are included to illustrate key concepts.
—
What Is Conductivity?
Conductivity (![]() ) is the measure of a material’s ability to conduct electric current. It is the reciprocal of resistivity (
) is the measure of a material’s ability to conduct electric current. It is the reciprocal of resistivity (![]() ), which measures a material’s opposition to current flow.
), which measures a material’s opposition to current flow.
The mathematical relationship is:
![]()
Where:
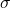 is the conductivity (siemens per meter, S/m).
is the conductivity (siemens per meter, S/m).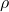 is the resistivity (
is the resistivity (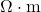 ).
).
Conductivity depends on the material’s composition, temperature, and structure. Metals, such as copper and silver, have high conductivity, while insulators, like rubber and glass, have low conductivity.
—
Units of Conductivity
SI Unit: Siemens per Meter (S/m)
In the International System of Units (SI), conductivity is measured in siemens per meter (S/m).
1 siemens (S) is the reciprocal of 1 ohm (![]() ):
):
![]()
Thus:
![]()
Example: Copper, a highly conductive material, has a conductivity of approximately:
![]()
—
CGS Unit: Reciprocal Ohm-Centimeter (Ω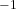 ·cm
·cm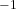 )
)
In the CGS system, conductivity is sometimes measured in reciprocal ohm-centimeters:
![]()
Example: A material with a conductivity of ![]() in SI units corresponds to:
in SI units corresponds to:
![]()
—
Relationship Between Conductivity, Current, and Electric Field
The conductivity of a material determines the current density (![]() ) produced by an electric field (
) produced by an electric field (![]() ). This relationship is given by Ohm’s Law in its microscopic form:
). This relationship is given by Ohm’s Law in its microscopic form:
![]()
Where:
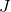 is the current density (
is the current density (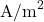 ).
).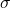 is the conductivity (
is the conductivity (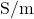 ).
).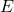 is the electric field (
is the electric field (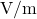 ).
).
Example: A material with conductivity ![]() and subjected to an electric field
and subjected to an electric field ![]() will have a current density:
will have a current density:
![]()
—
Factors Affecting Conductivity
1. Material Type:
- Conductors (e.g., copper, silver) have high conductivity.
- Insulators (e.g., rubber, glass) have low conductivity.
- Semiconductors (e.g., silicon) have intermediate and variable conductivity.
2. Temperature:
- In metals, conductivity decreases with increasing temperature due to increased electron scattering.
- In semiconductors, conductivity increases with temperature as more charge carriers are generated.
3. Impurities and Doping:
- Impurities in conductors generally reduce conductivity.
- Doping in semiconductors enhances conductivity by introducing additional charge carriers.
4. Material Structure:
- Crystalline materials have higher conductivity compared to amorphous materials due to better charge carrier mobility.
—
Measuring Conductivity
Conductivity is measured using techniques that apply an electric field to the material and measure the resulting current. The most common methods include:
1. Two-Probe and Four-Probe Methods
- Apply a voltage across a sample and measure the current.
- The resistance is calculated, and conductivity is derived using the sample’s geometry.
Example: A cylindrical conductor with length ![]() and cross-sectional area
and cross-sectional area ![]() , and resistance
, and resistance ![]() , has conductivity:
, has conductivity:
![]()
2. Inductive Methods
- Use electromagnetic induction to measure conductivity, especially for non-contact applications.
3. Electrochemical Impedance Spectroscopy
- Used in solutions to measure ionic conductivity, involving frequency-dependent analysis.
—
Real-World Examples of Conductivity
1. Metals: Electrical Wiring
Metals like copper and aluminum are widely used in electrical wiring due to their high conductivity.
- Example: Copper has a conductivity of
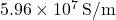 , making it an ideal choice for low-resistance electrical connections.
, making it an ideal choice for low-resistance electrical connections.
—
2. Semiconductors: Electronics
Semiconductors such as silicon and gallium arsenide have tunable conductivity, making them essential for transistors and diodes.
- Example: The conductivity of intrinsic silicon (
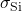 ) at room temperature is about
) at room temperature is about 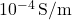 . Doping silicon with phosphorus increases its conductivity significantly, enabling its use in electronic devices.
. Doping silicon with phosphorus increases its conductivity significantly, enabling its use in electronic devices.
—
3. Ionic Solutions: Water Purification
Conductivity measurements in solutions indicate ion concentration, critical for water quality analysis.
- Example: Distilled water has low conductivity (
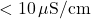 ) due to minimal ion presence, while seawater has high conductivity (
) due to minimal ion presence, while seawater has high conductivity (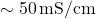 ) due to dissolved salts.
) due to dissolved salts.
—
4. Thermal Conductivity and Electrical Conductivity
In metals, high electrical conductivity often correlates with high thermal conductivity due to the Wiedemann-Franz law.
- Example: Silver has both the highest electrical and thermal conductivity among metals, used in specialized applications like high-frequency antennas.
—
5. Insulators: Dielectric Materials
Materials with very low conductivity, such as Teflon and rubber, are used as insulators to prevent current leakage.
- Example: Teflon has a conductivity near
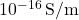 , making it ideal for coating electrical wires in high-voltage systems.
, making it ideal for coating electrical wires in high-voltage systems.
—
Applications of Conductivity
1. Electrical Engineering
- Conductivity determines material suitability for wires, connectors, and electronic components.
- Example: Copper is preferred in wiring due to its high conductivity.
2. Semiconductor Devices
- Controlled conductivity in semiconductors enables the creation of transistors, diodes, and integrated circuits.
3. Water Quality Monitoring
- Ionic conductivity is used to assess the purity of water in industries and environmental monitoring.
- Example: Conductivity sensors measure salinity in oceans and impurities in drinking water.
4. Corrosion Studies
- Conductivity measurements in electrolytes help predict and mitigate corrosion in industrial systems.
5. Battery Technology
- The performance of batteries depends on the conductivity of electrodes and electrolytes.
- Example: Lithium-ion batteries rely on materials with high ionic and electronic conductivity for efficient charge storage.
—
Conclusion
Conductivity is a critical property that characterizes how well materials and systems allow the flow of electric current. Measured in siemens per meter (S/m), it bridges the microscopic behavior of electrons and ions with macroscopic electrical properties. Understanding conductivity enables advancements in electronics, material science, and environmental monitoring, making it an indispensable concept in both theory and practice. From wiring in power systems to water quality sensors and semiconductor devices, the unit of conductivity underpins a wide array of technologies shaping the modern world.