Understanding the Work-Energy Theorem: Concepts and Applications

The Work-Energy Theorem is a fundamental principle in physics that establishes a direct relationship between the work done on an object and the change in its kinetic energy. This theorem plays a critical role in understanding motion, as it links the concepts of force, displacement, and energy. By examining how work influences an object’s energy, the Work-Energy Theorem provides insights into real-world phenomena ranging from vehicle acceleration to gravitational potential energy in free-falling objects.

In this article, we’ll delve into the Work-Energy Theorem, explore its mathematical formulation, discuss the types of work involved, and provide practical examples that demonstrate how the theorem applies in everyday situations.

The Concept of Work and Energy

Before diving into the Work-Energy Theorem, it is essential to understand the basics of work and energy in physics.

1. Work: In physics, work is done when a force causes displacement of an object. It is defined as the product of the force applied in the direction of the displacement and the distance traveled. The formula for work ( $W$ ) is:

$W = F \cdot d \cdot \cos(\theta)$

where:
– $F$ is the force applied,
– $d$ is the displacement, and
– $\theta$ is the angle between the direction of the force and the direction of displacement.

Work is measured in joules (J) in the International System of Units (SI).

2. Energy: Energy is the capacity to do work. Kinetic energy ( $KE$ ) is the energy possessed by a moving object due to its motion, and it is given by:

$KE = \frac{1}{2}mv^2$

where $m$ is the mass of the object and $v$ is its velocity.

Statement of the Work-Energy Theorem

The Work-Energy Theorem states that the net work done on an object is equal to the change in its kinetic energy. Mathematically, this can be expressed as:

$W_{\text{net}} = \Delta KE$

where:

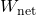$W_{\text{net}}$ is the total work done on the object, and
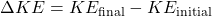$\Delta KE = KE_{\text{final}} - KE_{\text{initial}}$ is the change in kinetic energy.

In essence, the Work-Energy Theorem tells us that applying a net force to an object and causing it to move will result in a change in the object’s kinetic energy, proportional to the amount of work done.

Derivation of the Work-Energy Theorem

To understand the theorem further, let’s derive it from Newton’s Second Law of Motion and kinematic principles.

1. Starting with Newton’s Second Law: According to Newton’s Second Law,

$F_{\text{net}} = m \cdot a$

where $F_{\text{net}}$ is the net force applied to the object, $m$ is its mass, and $a$ is its acceleration.

2. Expressing Acceleration in Terms of Velocity: Acceleration can be expressed as the change in velocity over displacement:

$a = \frac{dv}{dt} = \frac{dv}{dx} \cdot \frac{dx}{dt} = v \cdot \frac{dv}{dx}$

3. Work Done by Net Force: The work done by the net force over a displacement $dx$ is:

$dW = F_{\text{net}} \cdot dx = m \cdot a \cdot dx$

Substituting $a = v \cdot \frac{dv}{dx}$ :

$dW = m \cdot v \cdot dv$

4. Integrating to Find Total Work: Integrate both sides with respect to the initial and final velocities:

$W_{\text{net}} = \int_{v_{\text{initial}}}^{v_{\text{final}}} m \cdot v \cdot dv$

$W_{\text{net}} = m \left[ \frac{v^2}{2} \right]_{v_{\text{initial}}}^{v_{\text{final}}}$

$W_{\text{net}} = \frac{1}{2} m v_{\text{final}}^2 - \frac{1}{2} m v_{\text{initial}}^2$

$W_{\text{net}} = KE_{\text{final}} - KE_{\text{initial}} = \Delta KE$

This derivation confirms that the net work done on an object is equal to the change in its kinetic energy, aligning with the Work-Energy Theorem.

Types of Work in the Work-Energy Theorem

1. Positive Work

Positive work occurs when the applied force and displacement are in the same direction, causing an increase in the object’s kinetic energy. For example, when pushing a car forward, the force applied and the car’s movement are in the same direction, resulting in a positive change in its kinetic energy.

2. Negative Work

Negative work occurs when the force opposes the direction of displacement, decreasing the object’s kinetic energy. An example is the work done by friction on a sliding object, which acts opposite to the movement, gradually reducing the object’s speed and, hence, its kinetic energy.

3. Zero Work

When the force applied is perpendicular to the direction of motion or when there is no displacement, no work is done. An example is an object moving in a circular path under a centripetal force; the centripetal force is perpendicular to the direction of motion, so it does no work.

Practical Applications of the Work-Energy Theorem

The Work-Energy Theorem is widely applicable across various physical scenarios. Below are some examples that demonstrate how the theorem applies in different situations.

Example 1: A Car Accelerating on a Straight Road

Imagine a car with a mass of 1,000 kg accelerating from a velocity of 10 m/s to 20 m/s along a straight road. We can calculate the net work done on the car during this acceleration using the Work-Energy Theorem.

1. Calculate Initial and Final Kinetic Energy:

$KE_{\text{initial}} = \frac{1}{2} m v_{\text{initial}}^2 = \frac{1}{2} \times 1000 \times (10)^2 = 50,000 \, \text{J}$

$KE_{\text{final}} = \frac{1}{2} m v_{\text{final}}^2 = \frac{1}{2} \times 1000 \times (20)^2 = 200,000 \, \text{J}$

2. Calculate the Change in Kinetic Energy:

$\Delta KE = KE_{\text{final}} - KE_{\text{initial}} = 200,000 - 50,000 = 150,000 \, \text{J}$

Thus, the net work done on the car to accelerate it from 10 m/s to 20 m/s is 150,000 J. This work could be provided by the engine through the force applied by the tires on the road.

Example 2: Braking a Moving Object

Consider a cyclist with a total mass of 80 kg (including the bike) traveling at a speed of 8 m/s. When the cyclist applies the brakes, frictional force does negative work on the system, reducing the kinetic energy to zero. We can calculate the work done by friction to stop the cyclist.

1. Initial Kinetic Energy:

$KE_{\text{initial}} = \frac{1}{2} m v^2 = \frac{1}{2} \times 80 \times (8)^2 = 2560 \, \text{J}$

2. Final Kinetic Energy: When the cyclist stops, $KE_{\text{final}} = 0$ .

3. Work Done by Friction:

$W_{\text{net}} = \Delta KE = KE_{\text{final}} - KE_{\text{initial}} = 0 - 2560 = -2560 \, \text{J}$

The negative work of 2560 J indicates that friction has removed energy from the system, bringing the cyclist to a halt.

Example 3: Free-Falling Object under Gravity

Consider a 2 kg stone dropped from a height of 10 m. When the stone reaches the ground, we can calculate the work done by gravity to determine its speed upon impact.

1. Potential Energy at Height:
The initial potential energy at a height $h$ is given by:

$PE = m \cdot g \cdot h = 2 \cdot 9.8 \cdot 10 = 196 \, \text{J}$

2. Applying the Work-Energy Theorem:
As the stone falls, gravity does positive work, converting potential energy into kinetic energy. By the time it reaches the ground, this work done equals the change in kinetic energy.

3. Kinetic Energy Upon Impact:
Since the stone starts from rest, $KE_{\ text{initial}} = 0$ . By the Work-Energy Theorem:

$W_{\text{net}} = \Delta KE = KE_{\text{final}} - KE_{\text{initial}} = 196 \, \text{J}$

Thus, the stone’s kinetic energy upon impact is 196 J. Using $KE = \frac{1}{2}mv^2$ , we can solve for $v$ :

$196 = \frac{1}{2} \times 2 \times v^2$

$v^2 = \frac{196}{1} = 196$

$v = \sqrt{196} = 14 \, \text{m/s}$

The stone hits the ground at a speed of 14 m/s, and the work done by gravity throughout the fall results in this final speed.

Limitations of the Work-Energy Theorem

The Work-Energy Theorem provides a straightforward way to analyze mechanical systems, but it has limitations:

Non-Conservative Forces: The theorem only applies directly to systems where forces are conservative. In the presence of non-conservative forces like air resistance, additional calculations are needed.
Rotational Motion: The theorem applies to translational motion, but rotational systems require a modified approach with rotational kinetic energy and torque.
Complex Interactions: Systems involving complex interactions among multiple objects may need a more detailed analysis of forces and energy transformations.

Conclusion

The Work-Energy Theorem is a fundamental tool in physics, allowing us to relate the work done on an object to changes in its kinetic energy. This principle not only clarifies the relationship between force, displacement, and energy but also has practical applications across various scenarios, such as vehicle acceleration, braking, and free-fall motion. Understanding the Work-Energy Theorem provides a foundational approach to analyzing and predicting the behavior of objects under force, simplifying calculations and offering valuable insights into real-world dynamics.