Understanding the Z-Score Table: A Guide to Standardized Normal Distribution

The Z-score table, also known as the standard normal distribution table, is a powerful statistical tool that shows the relationship between Z-scores (standardized values) and probabilities in a normal distribution. Z-scores help us understand how individual values relate to the mean of a data set, enabling us to calculate the probability of observing specific values and determine the likelihood of various outcomes.

In this article, we will explore the concept of Z-scores, how the Z-score table works, and walk through examples to illustrate its applications.

What is a Z-Score?

A Z-score represents the number of standard deviations a specific data point is from the mean of a data set. In other words, the Z-score tells us whether a value lies above or below the mean and by how many standard deviations. Z-scores can be positive or negative, where a positive Z-score indicates a value above the mean, and a negative Z-score indicates a value below the mean.

The formula for calculating a Z-score is:

$Z = \frac{X - \mu}{\sigma}$

where:

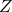$Z$ is the Z-score,
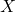$X$ is the data point,
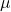$\mu$ is the mean of the data set, and
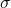$\sigma$ is the standard deviation of the data set.

Example:

Suppose we have a data set of exam scores with a mean ( $\mu$ ) of 75 and a standard deviation ( $\sigma$ ) of 10. If a student scored 85, we can calculate the Z-score as follows:

$Z = \frac{85 - 75}{10} = \frac{10}{10} = 1$

This Z-score of 1 indicates that the score of 85 is 1 standard deviation above the mean.

Understanding the Z-Score Table

The Z-score table helps us convert Z-scores into probabilities for a standard normal distribution. A standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1. By transforming data into Z-scores, we standardize different data sets, making them comparable across distributions.

In a Z-score table:

Each entry represents the probability that a value is less than or equal to a given Z-score.
The rows of the table show the first digit and first decimal place of the Z-score (e.g., 1.2).
The columns provide the second decimal place (e.g., 0.03).

The table value indicates the cumulative probability up to that Z-score, allowing us to determine the probability of a value occurring within certain ranges in a normal distribution.

Using the Z-Score Table

To use the Z-score table, follow these steps:

1. Calculate the Z-score for the data point.
2. Locate the row corresponding to the first decimal place of the Z-score.
3. Identify the column for the second decimal place.
4. Find the probability at the intersection of the row and column.

Example:

Let’s say we calculated a Z-score of 1.23 for a value, and we want to find the probability associated with this Z-score.

1. Locate the row for 1.2.
2. In the 1.2 row, find the column for 0.03.
3. The value at this intersection is 0.8907.

Thus, a Z-score of 1.23 corresponds to a cumulative probability of 0.8907, meaning there is an 89.07% chance that a randomly chosen value from this distribution will be less than or equal to this Z-score.

Working with Positive and Negative Z-Scores

In a standard normal distribution:

Positive Z-scores are above the mean, representing values to the right of the mean on the distribution curve.
Negative Z-scores are below the mean, representing values to the left of the mean on the distribution curve.

The Z-score table typically only shows positive Z-scores. For negative Z-scores, we use symmetry:

$P(Z \leq -z) = 1 - P(Z \leq z)$

Example:

If we have a Z-score of -1.23, we find the cumulative probability for 1.23 in the table, which is 0.8907. Then:

$P(Z \leq -1.23) = 1 - 0.8907 = 0.1093$

This means there is a 10.93% probability that a randomly chosen value will be less than a Z-score of -1.23.

Applications of Z-Scores and the Z-Score Table

1. Calculating Probabilities for Data Values

The Z-score table allows us to determine probabilities associated with specific data values, providing insights into how likely it is to observe a value within a given range.

Example:

Consider a company that records employee working hours with a mean of 40 hours per week and a standard deviation of 5 hours. If we want to know the probability that a randomly selected employee works less than 35 hours per week, we calculate the Z-score for 35:

$Z = \frac{35 - 40}{5} = -1$

Using the Z-score table, we find that $P(Z \leq -1) = 0.1587$ . Therefore, there is a 15.87% probability that an employee works fewer than 35 hours per week.

2. Finding Probabilities Between Two Z-Scores

The Z-score table also helps find probabilities between two Z-scores, allowing us to analyze data within specific ranges.

Example:

Using the previous example of employee working hours, suppose we want to find the probability that an employee works between 35 and 45 hours per week. We already know:

$P(Z \leq -1) = 0.1587 \quad \text{and} \quad P(Z \leq 1) = 0.8413$

To find the probability between these values, subtract the lower probability from the higher probability:

$P(-1 \leq Z \leq 1) = P(Z \leq 1) - P(Z \leq -1) = 0.8413 - 0.1587 = 0.6826$

This means there is a 68.26% probability that an employee works between 35 and 45 hours per week.

3. Identifying Outliers

In data analysis, outliers are values significantly different from the rest of the data set. Using Z-scores, we can identify outliers by checking if values lie outside a certain range, such as $|Z| > 2$ (about 95% of values fall within 2 standard deviations) or $|Z| > 3$ (about 99.7% of values fall within 3 standard deviations).

Example:

Suppose we are analyzing heights of adult males, with a mean height of 70 inches and a standard deviation of 3 inches. If someone’s height is 60 inches, we calculate the Z-score:

$Z = \frac{60 - 70}{3} = -3.33$

Since $|Z| > 3$ , this height is considered an outlier, as it is more than 3 standard deviations below the mean.

4. Standardizing Different Data Sets

Z-scores enable comparison of values across different data sets by standardizing scores to a common scale.

Example:

A student scores 80 on a math test with a mean of 75 and a standard deviation of 5, and 88 on a science test with a mean of 85 and a standard deviation of 4. To determine which score is relatively better, we calculate the Z-scores:

$Z_{\text{math}} = \frac{80 - 75}{5} = 1$

$Z_{\text{science}} = \frac{88 - 85}{4} = 0.75$

The math test Z-score of 1 indicates that this score is one standard deviation above the mean, while the science score Z-score is only 0.75 standard deviations above the mean. Thus, the student performed relatively better on the math test.

Cumulative Probabilities and Percentiles

The Z-score table provides cumulative probabilities that help identify percentiles within a normal distribution. For a Z-score of 0, the cumulative probability is 0.5 (or the 50th percentile), which divides the distribution symmetrically. Positive Z-scores correspond to percentiles above the mean, while negative Z-scores fall below the mean.

Example:

If a student’s test score has a Z-score of 1.65, the cumulative probability is 0.9505, or the 95th percentile. This means the student scored better than 95% of others in the same distribution.

Reverse Lookup: Finding Z-Scores for a Given Probability

Sometimes, we start with a known probability and want to find the corresponding Z-score. This is particularly useful for calculating confidence intervals in statistics.

Example:

If we want to find the Z-score corresponding to the 90th percentile, we look for a probability of 0.9000 in the Z-score table. The closest value is 0.8997, which corresponds to a Z-score of approximately 1.28. Thus,

the 90th percentile corresponds to a Z-score of 1.28.

Practical Application of Z-Scores in Hypothesis Testing

In hypothesis testing, Z-scores allow statisticians to determine whether sample means are significantly different from population means, assuming the null hypothesis. By comparing observed Z-scores to critical Z-scores, statisticians decide whether to reject the null hypothesis.

Example:

Suppose a company claims that its employees work an average of 40 hours per week. An auditor collects a sample with a mean of 38 hours and a standard deviation of 4 hours. For a sample of 30 employees, we calculate the Z-score:

$Z = \frac{38 - 40}{4/\sqrt{30}} = -2.74$

Using the Z-score table, a Z-score of -2.74 corresponds to a cumulative probability of approximately 0.0030. Since this probability is very low, the auditor might conclude that the actual average is likely less than 40 hours, providing evidence against the company’s claim.

Conclusion

The Z-score table is an invaluable tool in probability and statistics for determining probabilities, comparing data values, identifying outliers, and interpreting percentiles. Understanding how to use the Z-score table and interpret Z-scores provides a foundational skill for data analysis, enabling better insights and decision-making. With these concepts and examples, we gain the ability to analyze data more effectively and apply Z-scores across a wide range of fields, from business to science and social research.