Understanding Trigonometric Ratios: Concepts, Uses, and Examples

Trigonometry, derived from the Greek words for “triangle” and “measure,” is a branch of mathematics that studies the relationships between the sides and angles of triangles. One of the most fundamental concepts in trigonometry is the set of trigonometric ratios, which are used to analyze right triangles. These ratios—sine, cosine, tangent, along with their reciprocals, cosecant, secant, and cotangent—form the foundation for solving problems in geometry, physics, engineering, and various other fields.

In this article, we explore the key trigonometric ratios, their definitions, how to use them, and examples that demonstrate their applications in solving real-world problems. Whether you’re a student learning the basics or someone interested in practical applications, understanding trigonometric ratios is essential.

What Are Trigonometric Ratios?

Trigonometric ratios are mathematical relationships between the lengths of sides in a right triangle. These ratios help us understand how the angles of a triangle relate to its sides. The primary trigonometric ratios are:

1. Sine (sin)
2. Cosine (cos)
3. Tangent (tan)

These three ratios are defined based on the lengths of the sides of a right triangle, where one of the angles is $90^\circ$ . The sides of the triangle are defined as follows:

Hypotenuse: The longest side, opposite the right angle.
Opposite side: The side opposite the angle of interest.
Adjacent side: The side next to the angle of interest (but not the hypotenuse).

Trigonometric Ratio Definitions:

Sine ( $\sin$ ): $\sin(\theta) = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
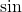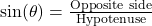
Cosine ( $\cos$ ): $\cos(\theta) = \frac{\text{Adjacent side}}{\text{Hypotenuse}}$
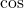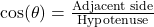
Tangent ( $\tan$ ): $\tan(\theta) = \frac{\text{Opposite side}}{\text{Adjacent side}}$

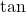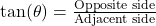
Example:
Suppose you have a right triangle where the angle $\theta$ is $30^\circ$ , the length of the hypotenuse is 10 units, and the length of the side adjacent to $\theta$ is 8.66 units. You can calculate the trigonometric ratios as follows:

$\sin(30^\circ) = \frac{\text{Opposite side}}{10} = \frac{5}{10} = 0.5$
$\cos(30^\circ) = \frac{8.66}{10} = 0.866$
$\tan(30^\circ) = \frac{5}{8.66} = 0.577$

These ratios are essential for solving triangles, especially when some sides or angles are unknown.

The Reciprocal Trigonometric Ratios

In addition to the three primary trigonometric ratios, there are also three reciprocal ratios:
1. Cosecant (csc): $\csc(\theta) = \frac{1}{\sin(\theta)} = \frac{\text{Hypotenuse}}{\text{Opposite side}}$
2. Secant (sec): $\sec(\theta) = \frac{1}{\cos(\theta)} = \frac{\text{Hypotenuse}}{\text{Adjacent side}}$
3. Cotangent (cot): $\cot(\theta) = \frac{1}{\tan(\theta)} = \frac{\text{Adjacent side}}{\text{Opposite side}}$

Example:
Continuing with our previous triangle:

$\csc(30^\circ) = \frac{1}{\sin(30^\circ)} = \frac{1}{0.5} = 2$
$\sec(30^\circ) = \frac{1}{\cos(30^\circ)} = \frac{1}{0.866} \approx 1.155$
$\cot(30^\circ) = \frac{1}{\tan(30^\circ)} = \frac{1}{0.577} \approx 1.732$

These reciprocal functions are particularly useful in advanced trigonometric equations and calculus.

Using Trigonometric Ratios to Solve Right Triangles

One of the primary uses of trigonometric ratios is solving right triangles, which involves finding unknown side lengths or angles. The trigonometric ratios provide a straightforward way to relate the sides and angles, allowing us to solve for missing information.

Example 1: Finding a Side Length
Imagine a scenario where you need to determine the height of a tree, but you can’t measure it directly. You stand 30 meters away from the base of the tree and measure the angle of elevation to the top as $45^\circ$ .

To find the height of the tree ( $h$ ):

You can use the tangent ratio: $\tan(45^\circ) = \frac{\text{Opposite}}{\text{Adjacent}}$
$\tan(45^\circ) = 1$ , so: $1 = \frac{h}{30}$
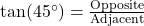
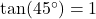Solving for 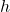$h$ , you get 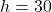$h = 30$ meters.

Example 2: Finding an Angle
Suppose you know the lengths of two sides of a right triangle: the opposite side is 7 units, and the hypotenuse is 10 units. To find the angle $\theta$ :

Use the sine ratio: $\sin(\theta) = \frac{7}{10} = 0.7$
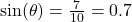
To find 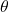$\theta$ , use the inverse sine function: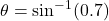 $\theta = \sin^{-1}(0.7)$
Using a calculator, $\theta \approx 44.4^\circ$ .

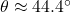Applications of Trigonometric Ratios in Real Life

Trigonometric ratios are not just theoretical concepts; they have practical applications in various fields such as engineering, architecture, physics, and even art. Here are a few real-world applications:

1. Construction and Architecture
Builders and architects use trigonometry to determine the correct angles and lengths for constructing buildings, bridges, and roads. For example, when designing a roof, they need to calculate the correct angle for the roof slope to ensure proper drainage and stability.

*Example*:
An architect needs to design a ramp for wheelchair access that rises to a height of 1.5 meters over a distance of 6 meters. To determine the angle of elevation ( $\theta$ ):

$\sin(\theta) = \frac{1.5}{6}$
$\sin(\theta) = 0.25$
$\theta = \sin^{-1}(0.25) \approx 14.5^\circ$

2. Navigation and Aviation
Pilots use trigonometric ratios to determine flight paths, calculate distances, and adjust altitudes. Trigonometry helps them navigate using angles of elevation and depression when approaching runways or navigating around obstacles.

*Example*:
A pilot flying at an altitude of 2,000 meters needs to descend to a runway located 10 kilometers away. The angle of descent ( $\theta$ ) can be calculated using:

$\tan(\theta) = \frac{2000}{10000} = 0.2$
$\theta = \tan^{-1}(0.2) \approx 11.3^\circ$

3. Physics and Engineering
In physics, trigonometric ratios are used to analyze waveforms, electrical circuits, and oscillations. Engineers use these ratios to calculate forces, tensions, and trajectories in mechanical systems.

*Example*:
In electrical engineering, the phase angle between voltage and current can be determined using the cosine function. For instance, if the power factor (cosine of the phase angle) of a circuit is 0.8, you can find the phase angle ( $\theta$ ) as:

$\theta = \cos^{-1}(0.8) \approx 36.9^\circ$

Trigonometric Ratios in the Unit Circle

Understanding trigonometric ratios also involves the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate system. The unit circle is fundamental in trigonometry because it relates angles to the coordinates of points on the circle.

Key Points:

For any angle 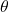$\theta$ , the coordinates of the point where the terminal side of the angle intersects the unit circle are $(\cos(\theta), \sin(\theta))$ .
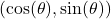The tangent of the angle is given by $\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$ .

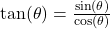Example:
If $\theta = 60^\circ$ :

$\cos(60^\circ) = \frac{1}{2}$
$\sin(60^\circ) = \frac{\sqrt{3}}{2}$
$\tan(60^\circ) = \frac{\sin(60^\circ)}{\cos(60^\circ)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}$

The unit circle helps visualize how trigonometric functions behave

as the angle increases beyond $90^\circ$ , covering all four quadrants of the circle.

Conclusion: Mastering Trigonometric Ratios

Trigonometric ratios are fundamental tools in mathematics, with applications that extend far beyond solving triangles. From designing buildings and flying planes to analyzing waves and circuits, these ratios are indispensable in science, engineering, and technology.

By mastering the basics of sine, cosine, and tangent, along with their reciprocals and applications in the unit circle, you can solve complex problems and gain a deeper understanding of the mathematical relationships that govern the physical world. Whether you’re a student, an engineer, or simply someone fascinated by math, trigonometric ratios offer a gateway to exploring the elegant structure of geometry and its real-world applications.