Understanding Uniform Circular Motion: Concepts and Applications

Uniform Circular Motion (UCM) describes the motion of an object traveling along a circular path at a constant speed. Despite the speed remaining constant, the direction of motion continuously changes, leading to acceleration. This unique type of motion is fundamental in physics and appears in various natural and engineered systems, such as planetary orbits, the rotation of wheels, and artificial satellites.

In this article, we’ll explore the principles, mathematical descriptions, and real-world examples of uniform circular motion to provide a comprehensive understanding of the concept.

What Is Uniform Circular Motion?

Uniform Circular Motion occurs when an object moves in a circular path with a constant speed. While the speed (magnitude of velocity) is unchanging, the velocity vector, which depends on both magnitude and direction, varies because the object continuously changes direction. This variation introduces centripetal acceleration, which keeps the object moving along the circular path.

Key Features of Uniform Circular Motion

1. Constant Speed: The magnitude of the object’s velocity remains constant.
2. Changing Velocity: The direction of motion changes at every instant, causing acceleration.
3. Centripetal Force: A force directed toward the center of the circle acts on the object, maintaining the circular motion.
4. Circular Path: The trajectory is a perfect circle, with the object equidistant from the center at all times.

Example: A car moving around a circular track at a constant speed is an example of uniform circular motion. Although the speedometer reads a constant value, the direction of motion changes continuously.

Centripetal Force and Centripetal Acceleration

To maintain uniform circular motion, a force must constantly act on the object, directing it toward the center of the circle. This force is known as centripetal force, and it is responsible for the object’s inward acceleration, called centripetal acceleration.

Centripetal Acceleration

The centripetal acceleration ( $a_c$ ) of an object moving in a circle is given by:

$a_c = \frac{v^2}{r}$

Where:

$v$ = Speed of the object
$r$ = Radius of the circular path

This acceleration points toward the center of the circle and is perpendicular to the object’s instantaneous velocity.

Example: A stone tied to a string and whirled in a circular motion experiences centripetal acceleration, which keeps it in the circular path. If the string breaks, the stone will fly off tangentially because there is no force to redirect its motion.

Centripetal Force

The centripetal force ( $F_c$ ) required to maintain circular motion is given by:

$F_c = m \cdot a_c = \frac{m \cdot v^2}{r}$

Where:

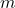$m$ = Mass of the object
$v$ = Speed of the object
$r$ = Radius of the circular path

Centripetal force can arise from various sources, such as gravity, tension, friction, or electromagnetic forces.

Example:

For a car turning on a circular road, friction between the tires and the road provides the centripetal force.
For a planet orbiting the sun, gravitational force acts as the centripetal force.

Angular Velocity and Period in Circular Motion

In addition to linear velocity, circular motion involves angular quantities that describe the rotation of the object.

Angular Velocity

The angular velocity ( $\omega$ ) measures how quickly an object rotates around the circle and is defined as:

$\omega = \frac{\theta}{t}$

Where:

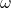$\omega$ = Angular velocity (radians per second)
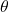$\theta$ = Angle swept by the object (radians)
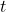$t$ = Time taken to sweep the angle

Angular velocity relates to linear velocity ( $v$ ) by the formula:

$v = \omega \cdot r$

Example: A Ferris wheel rotating at a rate of 2 radians per second with a radius of 10 meters has a linear velocity of:

$v = \omega \cdot r = 2 \cdot 10 = 20 \, \text{m/s}.$

Period and Frequency

The period ( $T$ ) is the time taken for one complete revolution, and the frequency ( $f$ ) is the number of revolutions per second. They are related as:

$f = \frac{1}{T}$

Angular velocity is also related to the period by:

$\omega = \frac{2\pi}{T}$

Example: A satellite orbiting Earth with a period of 90 minutes completes:

$f = \frac{1}{T} = \frac{1}{90 \times 60} = 0.000185 \, \text{Hz}.$

Energy in Uniform Circular Motion

While the speed of an object in uniform circular motion remains constant, its kinetic energy is constant as well:

$KE = \frac{1}{2} m v^2$

However, work done by centripetal force is zero because the force is perpendicular to the direction of motion. Thus, no energy is transferred in the direction of motion.

Example: An electron orbiting the nucleus in a hydrogen atom exhibits constant kinetic energy due to its uniform circular motion.

Real-World Examples of Uniform Circular Motion

1. Planetary Orbits

Planets orbit the sun in nearly circular paths due to the gravitational force acting as the centripetal force. For Earth, the speed of revolution remains nearly constant, ensuring a year-long orbit.

Example: Earth travels at an average orbital speed of about 29.78 km/s. Despite this high speed, it doesn’t escape the sun’s gravitational pull due to the inward centripetal force.

—

2. Amusement Park Rides

Rides like merry-go-rounds or Ferris wheels provide excellent examples of uniform circular motion. The centripetal force here is supplied by tension in the supporting cables or the structure of the ride.

Example: A person sitting on a rotating swing in an amusement park experiences a centripetal force provided by the chain. If the swing rotates faster, the tension in the chain increases to maintain the motion.

—

3. Artificial Satellites

Satellites in orbit around Earth follow circular paths at constant speeds. The centripetal force in this case is provided by Earth’s gravitational pull.

Example: The International Space Station (ISS) orbits Earth at an average speed of 7.66 km/s. Its centripetal force comes from Earth’s gravitational attraction.

—

4. Rotating Tires

The motion of a point on the edge of a spinning tire illustrates uniform circular motion. Although the tire rotates at a constant speed, any point on its circumference changes direction continuously.

Example: A car traveling at 72 km/h has wheels with a radius of 0.5 meters. The angular velocity of the wheel is calculated as:

$\omega = \frac{v}{r} = \frac{72 \times 1000 / 3600}{0.5} = 40 \, \text{rad/s}.$

—

5. Centrifuges

Centrifuges used in laboratories or industries involve uniform circular motion to separate components based on density. The high-speed rotation generates a strong centripetal force, which pushes denser materials outward.

Example: A centrifuge spinning at 10,000 revolutions per minute (rpm) has a very high angular velocity, creating enough force to separate blood components in medical testing.

—

Practical Implications and Importance

1. Space Exploration: Understanding uniform circular motion is crucial for designing satellite orbits and space missions.
2. Engineering: Circular motion principles are applied in designing rotating machinery, turbines, and flywheels.
3. Safety: Vehicle dynamics during turns rely on the balance between friction and centripetal force to prevent skidding.
4. Amusement Rides: The comfort and safety of circular rides depend on precise control of centripetal force and acceleration.

—

Conclusion

Uniform Circular Motion is a fascinating and essential concept in physics, describing the motion of objects along circular paths at constant speed. The interplay of centripetal force, acceleration, and velocity makes this motion unique. From planetary orbits and satellite trajectories to amusement park rides and centrifuges, UCM finds applications in countless areas of science and technology. By understanding its principles and mathematical relationships, we gain insight into the behavior of rotating systems and the forces that govern them, enhancing both theoretical and practical knowledge.