A Venn diagram is a graphical tool that represents sets and their relationships using overlapping circles. Named after British logician John Venn, Venn diagrams are used extensively in mathematics, logic, statistics, computer science, and even in everyday problem-solving. They offer a visual way to show relationships between groups, making it easier to identify shared and distinct elements among sets. In this article, we’ll explore the basics of Venn diagrams, their structure, types, and how they can be used effectively, with examples to illustrate each concept.
Basics of Venn Diagrams
A Venn diagram consists of circles or other shapes that represent different sets. These shapes overlap in ways that show the relationships among the sets, including intersections, unions, differences, and complements. Each area of the diagram represents a particular combination of elements, making it easy to visualize complex relationships.
Elements of a Venn Diagram
- Set: A collection of objects or elements. In a Venn diagram, each set is typically represented by a circle.
- Universal Set (U): The set that contains all possible elements relevant to the context. It is usually represented by a rectangle around the Venn diagram.
- Intersection ( ∩ ): The area where two or more sets overlap, representing elements common to all overlapping sets.
- Union ( ∪ ): The combination of all elements from the involved sets, whether or not they are shared.
- Complement: The elements in the universal set that are not in a specific set, represented by areas outside the set’s circle.
Basic Venn Diagram Notation
If we have two sets, ![]() and
and ![]() , the basic notations for Venn diagrams include:
, the basic notations for Venn diagrams include:
1. Union (![]() ): All elements that are in either
): All elements that are in either ![]() ,
, ![]() , or both.
, or both.
2. Intersection (![]() ): Elements that are in both
): Elements that are in both ![]() and
and ![]() .
.
3. Difference (![]() or
or ![]() ): Elements that are in
): Elements that are in ![]() but not in
but not in ![]() .
.
4. Complement (![]() ): Elements that are not in
): Elements that are not in ![]() .
.
Constructing a Venn Diagram
To construct a Venn diagram, start by drawing circles to represent each set, ensuring that they overlap if there are shared elements between sets. Each circle is labeled with the name of the set it represents. The universal set is often depicted as a rectangle surrounding all circles.
Example 1: Venn Diagram for Two Sets
Suppose we have two sets, ![]() and
and ![]() :
:
- Set
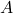 : {1, 2, 3, 4}
: {1, 2, 3, 4} - Set
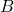 : {3, 4, 5, 6}
: {3, 4, 5, 6}
In this example:
- The intersection (
 ) is {3, 4}, as these are the elements common to both sets.
) is {3, 4}, as these are the elements common to both sets. - The union (
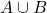 ) is {1, 2, 3, 4, 5, 6}, including all unique elements from both sets.
) is {1, 2, 3, 4, 5, 6}, including all unique elements from both sets. - The difference (
 ) is {1, 2}, which includes elements in
) is {1, 2}, which includes elements in 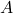 but not in
but not in 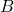 .
.
Drawing the Venn diagram:
1. Draw two overlapping circles labeled ![]() and
and ![]() .
.
2. Place the numbers 3 and 4 in the overlapping area to represent the intersection.
3. Place the numbers 1 and 2 in the part of ![]() that does not overlap with
that does not overlap with ![]() .
.
4. Place the numbers 5 and 6 in the part of ![]() that does not overlap with
that does not overlap with ![]() .
.
This simple Venn diagram visually illustrates the relationships between sets ![]() and
and ![]() and makes it easy to identify shared and unique elements.
and makes it easy to identify shared and unique elements.
Types of Venn Diagrams
Venn diagrams can represent relationships among multiple sets, and the more sets involved, the more complex the diagram becomes. Common types include:
1. Two-Set Venn Diagram
A two-set Venn diagram, like the example above, involves two overlapping circles, making it ideal for comparing two groups. It visually represents intersections, unions, and differences between two sets.
Example: Suppose we compare two sets of students—those who play soccer and those who play basketball. The two-set Venn diagram shows the students who play only soccer, only basketball, and both sports.
2. Three-Set Venn Diagram
A three-set Venn diagram consists of three overlapping circles, allowing for a more complex analysis of relationships among three sets.
Example: Imagine three sets representing students who study math, science, and history. The three-set Venn diagram shows students who study only one subject, any two subjects, or all three subjects. This type of diagram is useful for visualizing multiple levels of overlap.
3. Four-Set and Higher Venn Diagrams
Four-set Venn diagrams and those involving even more sets are more complex and are typically used in advanced fields like logic, probability, and statistics. These diagrams involve intricate patterns of overlapping areas, representing every possible combination of elements.
In practice, visualizing more than four sets in a Venn diagram can become difficult, and alternative visual tools like Euler diagrams may be used instead.
Applications of Venn Diagrams
Venn diagrams are versatile tools with applications in various fields, including:
1. Mathematics and Set Theory
Venn diagrams are fundamental in set theory, helping mathematicians visually demonstrate relationships between sets. They are particularly useful for teaching concepts like unions, intersections, and complements.
Example: Suppose we have two sets: even numbers and prime numbers. A Venn diagram can illustrate the overlap (even prime numbers) and the elements unique to each set.
2. Probability and Statistics
In probability, Venn diagrams help illustrate probabilities and conditional probabilities, allowing analysts to visualize the likelihood of overlapping events.
Example: Imagine rolling a die and recording the outcomes. Set ![]() could represent the event of rolling an even number, and set
could represent the event of rolling an even number, and set ![]() the event of rolling a number greater than 3. A Venn diagram shows the overlap of these events, making it easier to calculate probabilities such as
the event of rolling a number greater than 3. A Venn diagram shows the overlap of these events, making it easier to calculate probabilities such as ![]() or
or ![]() .
.
3. Computer Science and Logic
In computer science, Venn diagrams are used in logic, database querying, and information retrieval to show relationships among categories and criteria.
Example: In a database, a three-set Venn diagram could represent users who have purchased different products—say Product A, Product B, and Product C. This visualization can help analyze overlapping customer segments and inform targeted marketing strategies.
4. Decision-Making and Problem Solving
Venn diagrams are valuable in decision-making because they clearly organize information. They are often used in business, management, and personal decision-making.
Example: A business owner deciding on a location for a new store might use a Venn diagram to compare areas with high foot traffic, low rental costs, and proximity to competitors, identifying an ideal location that meets multiple criteria.
5. Biology and Medicine
In biology, Venn diagrams are used to classify species, compare genetic traits, and study overlapping medical conditions.
Example: Scientists may use a Venn diagram to study the distribution of diseases within different age groups or populations. Each set could represent people with a particular condition, and the overlapping areas could reveal commonalities.
Working with Venn Diagrams: An Example
To illustrate how Venn diagrams can be used for practical analysis, let’s work through a detailed example involving three sets.
Example: Analyzing Survey Data with a Three-Set Venn Diagram
Suppose a survey was conducted among 100 people about their preferences for three types of food: pizza, burgers, and sushi.
Define the sets as follows:
- Set
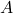 : People who like pizza
: People who like pizza - Set
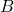 : People who like burgers
: People who like burgers - Set
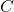 : People who like sushi
: People who like sushi
The survey results indicate:
- 40 people like pizza.
- 30 people like burgers.
- 25 people like sushi.
- 10 people like both pizza and burgers.
- 8 people like both pizza and sushi.
- 5 people like both burgers and sushi.
- 2 people like all three types of food.
Using this information, we can construct a Venn diagram to visualize the overlap between these preferences.
Steps for Constructing the Diagram
1. Draw three overlapping circles for sets ![]() ,
, ![]() , and
, and ![]() .
.
2. Label each region with the survey data:
– The central region, representing people who like all three foods (pizza, burgers, and sushi), contains 2 people.
– The area representing people who like both pizza and burgers, but not sushi, has ![]() people.
people.
– The area representing people who like both pizza and sushi, but not burgers, has ![]() people.
people.
– The area representing people who like both burgers and sushi, but not pizza, has ![]() people.
people.
3. Place the remaining counts in the individual areas:
– For pizza only: ![]() .
.
– For burgers only: ![]() .
.
– For sushi only: ![]() .
.
The Venn diagram visually represents how the preferences overlap, helping us understand the distribution of preferences among the respondents.
Benefits and Limitations of Venn Diagrams
Benefits
- Visual Clarity: Venn diagrams make complex relationships easier to understand.
- Organized Comparison: They allow us to compare multiple sets in a structured way.
- Versatility: Venn diagrams are used in diverse fields, from education to scientific research.
Limitations
- Complexity with Multiple Sets: As the number of sets increases, the diagram becomes harder to read.
- Limited Quantitative Analysis: Venn diagrams are best for visualizing relationships, not for precise numerical analysis.
Conclusion
Venn diagrams are powerful tools for visualizing relationships among sets, providing clarity in areas as diverse as mathematics, logic, computer science, and everyday decision-making. By understanding the basics of how Venn diagrams work—through concepts like union, intersection, and complement—and applying them in real-world contexts, we can organize information, solve problems, and make informed decisions. Whether analyzing survey data or comparing product features, Venn diagrams help us break down complex relationships and gain insights at a glance.