Uniform Motion and Non-Uniform Motion: Concepts, Differences, and Applications

Motion is a fundamental concept in physics that describes the change in position of an object over time. Understanding motion helps us analyze the behavior of objects in various scenarios, from everyday activities to complex engineering systems. Two primary types of motion are uniform motion and non-uniform motion, which differ based on how the speed or velocity of an object changes over time.

This article explains the principles of uniform and non-uniform motion, highlights their differences, and provides examples to illustrate their real-world applications.

What Is Uniform Motion?

Uniform motion occurs when an object travels equal distances in equal intervals of time, irrespective of the duration of the motion. In this type of motion, the object moves at a constant speed, and there is no change in its velocity. Since the velocity remains constant, the acceleration (rate of change of velocity) is zero in uniform motion.

Key Characteristics of Uniform Motion

1. Constant Speed: The object maintains the same speed throughout its motion.
2. Zero Acceleration: There is no change in velocity, so the acceleration is zero.
3. Straight-Line Path: The object typically moves in a straight line.

Mathematical Representation

If an object moves at a constant velocity $v$ over time $t$ , the distance $s$ traveled can be expressed as:

$s = v \cdot t$

where:

$s$ is the distance,
$v$ is the constant velocity,
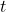$t$ is the time.

Example of Uniform Motion

Example: A car traveling on a straight highway at a constant speed of 60 km/h represents uniform motion. If the car maintains this speed for 2 hours, it will cover a distance of:

$s = v \cdot t = 60 \, \text{km/h} \times 2 \, \text{h} = 120 \, \text{km}.$

This predictable motion helps drivers estimate travel times accurately.

What Is Non-Uniform Motion?

Non-uniform motion occurs when an object travels unequal distances in equal intervals of time. In this type of motion, the speed or velocity of the object changes over time, resulting in acceleration or deceleration.

Key Characteristics of Non-Uniform Motion

1. Variable Speed: The object’s speed changes during its motion.
2. Non-Zero Acceleration: The velocity is not constant, so the object experiences acceleration (positive or negative).
3. Curved or Irregular Path: The object’s trajectory may not be a straight line, especially in cases involving directional changes.

Mathematical Representation

For non-uniform motion, the velocity ( $v$ ) is not constant. The instantaneous velocity at any given time is determined by the derivative of the position ( $s$ ) with respect to time ( $t$ ):

$v = \frac{ds}{dt}$

The acceleration ( $a$ ) is calculated as the rate of change of velocity:

$a = \frac{dv}{dt}$

Example of Non-Uniform Motion

Example: A roller coaster moving along a track exhibits non-uniform motion. Its speed increases as it descends and decreases as it ascends. For instance:

At the start, the roller coaster may accelerate from 0 m/s to 20 m/s in 5 seconds.
The acceleration can be calculated as:

$a = \frac{v_f - v_i}{t} = \frac{20 \, \text{m/s} - 0 \, \text{m/s}}{5 \, \text{s}} = 4 \, \text{m/s}^2.$

Differences Between Uniform and Non-Uniform Motion

The following table summarizes the key differences between uniform motion and non-uniform motion:

Feature	Uniform Motion	Non-Uniform Motion
Speed	Constant	Varies
Acceleration	Zero	Non-zero
Distance-Time Graph	Straight line with constant slope	Curved line indicating variable slope
Path	Usually a straight line	Can be curved or irregular
Equation of Motion	$\cdot t$	Involves calculus or kinematic equations

Graphical Representation

Uniform Motion: The distance-time graph for uniform motion is a straight line, indicating a constant rate of motion.
Non-Uniform Motion: The distance-time graph for non-uniform motion is a curve, reflecting changes in speed or velocity over time.

Applications of Uniform and Non-Uniform Motion

Understanding these two types of motion has practical applications in transportation, engineering, sports, and natural phenomena.

1. Transportation

Uniform motion is used to design systems for efficient travel, while non-uniform motion analysis helps ensure safety and optimize performance.

Uniform Motion Example: Cruise control in cars maintains a constant speed, achieving uniform motion on highways.
Non-Uniform Motion Example: Analyzing acceleration and deceleration patterns helps improve braking systems and vehicle dynamics.

2. Engineering and Robotics

Robotic systems and industrial machines often operate using principles of uniform motion for precision tasks and non-uniform motion for complex operations.

Uniform Motion Example: Conveyor belts in manufacturing plants move at a constant speed to ensure uniform processing.
Non-Uniform Motion Example: Robotic arms use non-uniform motion to accelerate and decelerate as they pick up or place objects.

3. Sports and Athletics

Athletes’ movements often involve non-uniform motion, as they accelerate, decelerate, or change direction during play.

Uniform Motion Example: A long-distance runner maintaining a steady pace over a flat course exhibits uniform motion.
Non-Uniform Motion Example: A sprinter accelerating at the start of a race and decelerating at the finish demonstrates non-uniform motion.

4. Natural Phenomena

Natural occurrences like falling objects and planetary orbits involve both types of motion.

Uniform Motion Example: Light traveling through a vacuum at a constant speed of 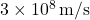$3 \times 10^8 \, \text{m/s}$ is an example of uniform motion.
Non-Uniform Motion Example: A free-falling object accelerates due to gravity, exemplifying non-uniform motion.

—

Example Problems

Example 1: Uniform Motion

Problem: A cyclist travels at a constant speed of 15 m/s for 10 seconds. How far does the cyclist travel?

Solution:
Using the formula:

$s = v \cdot t$

Substitute the values:

$s = 15 \, \text{m/s} \times 10 \, \text{s} = 150 \, \text{m}.$

The cyclist travels $150 \, \text{m}$ .

—

Example 2: Non-Uniform Motion

Problem: A car accelerates from 10 m/s to 30 m/s in 5 seconds. What is the car’s acceleration?

Solution:
Using the formula:

$a = \frac{v_f - v_i}{t}$

Substitute the values:

$a = \frac{30 \, \text{m/s} - 10 \, \text{m/s}}{5 \, \text{s}} = \frac{20 \, \text{m/s}}{5 \, \text{s}} = 4 \, \text{m/s}^2.$

The car’s acceleration is $4 \, \text{m/s}^2$ .

—

Conclusion

Uniform and non-uniform motion are two foundational concepts in kinematics that describe how objects move through space and time. Uniform motion involves constant speed and zero acceleration, while non-uniform motion includes varying speed or velocity and non-zero acceleration. Recognizing the differences between these types of motion and understanding their real-world applications help us analyze and design systems ranging from transportation and engineering to sports and natural phenomena. By applying these principles, scientists and engineers continue to optimize technology and explore the dynamics of motion in the universe.