What Is a Wave Function? – en-www.sridianti.com

The wave function is a fundamental concept in quantum mechanics that describes the quantum state of a particle or system. It is typically represented by the Greek letter $\psi$ (psi) and provides information about the probabilities of finding a particle in a particular state or location. The wave function is a mathematical representation, often a complex-valued function, that encapsulates all the information about a quantum system.

The wave function does not directly describe physical reality in the classical sense but instead encodes probabilities. Its interpretation has profound implications for understanding the nature of matter and energy at microscopic scales. This article explores the concept of the wave function, its mathematical framework, physical interpretation, and examples to illustrate its significance.

—

Mathematical Representation of the Wave Function

A wave function $\psi(x, t)$ is a function of position $x$ and time $t$ . It is generally a complex-valued function and is often written as:

$\psi(x, t) = A \cdot e^{i(kx - \omega t)},$

where:

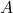$A$ : Amplitude of the wave function.
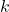$k$ : Wave number, related to the particle’s momentum.
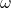$\omega$ : Angular frequency, related to the particle’s energy.
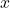$x$ : Position.
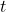$t$ : Time.

The wave function evolves over time according to the Schrödinger equation:

$i\hbar \frac{\partial \psi}{\partial t} = \hat{H} \psi,$

where:

$i$ : Imaginary unit.
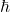$\hbar$ : Reduced Planck’s constant.
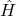$\hat{H}$ : Hamiltonian operator, representing the total energy of the system.

—

Physical Interpretation of the Wave Function

The wave function itself is not directly observable; instead, its square modulus, $|\psi(x, t)|^2$ , represents the probability density of finding the particle at position $x$ and time $t$ . This interpretation is known as the Born rule.

Example: Particle in a Box

Consider a particle confined to a one-dimensional box of length $L$ . The wave function for such a system is given by:

$\psi_n(x) = \sqrt{\frac{2}{L}} \sin\left(\frac{n\pi x}{L}\right),$

where $n$ is a quantum number that determines the energy state of the particle. The probability density is:

$|\psi_n(x)|^2 = \frac{2}{L} \sin^2\left(\frac{n\pi x}{L}\right).$

This shows that the particle is more likely to be found in regions where the sine function is large and less likely in regions where it is near zero.

—

Key Properties of the Wave Function

The wave function has several important properties that define its behavior and utility in quantum mechanics.

1. Normalization

The wave function must be normalized so that the total probability of finding the particle in all space is equal to 1:

$\int_{-\infty}^{\infty} |\psi(x, t)|^2 dx = 1.$

Example:
For the particle-in-a-box system, the normalization condition ensures that:

$\int_{0}^{L} \left(\frac{2}{L} \sin^2\left(\frac{n\pi x}{L}\right)\right) dx = 1.$

2. Superposition Principle

The wave function can exist as a linear combination (superposition) of multiple states:

$\psi(x, t) = c_1 \psi_1(x, t) + c_2 \psi_2(x, t),$

where $c_1$ and $c_2$ are coefficients. This principle explains phenomena like quantum interference.

Example:
In the double-slit experiment, the wave function of a particle passing through two slits combines, creating an interference pattern on the detection screen.

3. Continuity

The wave function and its first derivative must be continuous for physically meaningful solutions. Discontinuities would imply infinite energies, which are not possible in physical systems.

Example:
For a particle encountering a potential step, the wave function smoothly transitions between regions of different potentials.

—

Types of Wave Functions

The specific form of a wave function depends on the quantum system and the conditions it is subjected to.

1. Free Particle Wave Function

For a free particle with no external forces, the wave function takes the form of a plane wave:

$\psi(x, t) = A e^{i(kx - \omega t)}.$

Example:
An electron moving in empty space can be described by a free-particle wave function, indicating uniform probability across all space.

2. Bound State Wave Function

For particles confined to a potential, such as electrons in an atom, the wave function is localized and discrete. These wave functions often have specific shapes and quantized energy levels.

Example:
In the hydrogen atom, the wave function is given by solutions to the Schrödinger equation in spherical coordinates. The ground state wave function is:

$\psi_{100}(r, \theta, \phi) = \frac{1}{\sqrt{\pi a_0^3}} e^{-r/a_0},$

where $a_0$ is the Bohr radius.

3. Time-Dependent Wave Function

Time-dependent wave functions describe systems where the quantum state evolves over time.

Example:
A Gaussian wave packet describing a particle’s position uncertainty spreads out as time progresses, showing the dynamic nature of the wave function.

—

Applications of the Wave Function

The wave function is crucial for solving a variety of quantum problems and understanding phenomena in modern physics and technology.

1. Quantum Tunneling

The wave function predicts that particles can pass through energy barriers higher than their own energy, a phenomenon known as tunneling.

Example:
Tunneling explains how electrons pass through barriers in semiconductors, enabling devices like tunnel diodes and flash memory.

2. Atomic and Molecular Structure

Wave functions determine the behavior of electrons in atoms and molecules, explaining chemical bonding and molecular shapes.

Example:
The bonding in a hydrogen molecule is described by the overlap of the wave functions of two hydrogen atoms, forming a molecular orbital.

3. Quantum Computing

Quantum computers utilize superposition and entanglement of wave functions to perform computations.

Example:
A qubit’s state is represented by a superposition of wave functions, enabling parallel computation of multiple possibilities.

—

Wave Function Collapse

When a measurement is made, the wave function collapses to a single eigenstate corresponding to the observed value. Before the measurement, the wave function represents a superposition of possible outcomes.

Example:
In Schrödinger’s cat thought experiment, the wave function represents a superposition of the cat being alive and dead. Measurement collapses the wave function to one of these states.

—

Limitations and Interpretations of the Wave Function

The wave function is central to quantum mechanics, but its exact nature is subject to interpretation.

1. Copenhagen Interpretation

The Copenhagen interpretation posits that the wave function represents probabilities and collapses upon measurement. It emphasizes the role of observation in defining quantum states.

Example:
An electron’s position is described by a probability cloud until measured, at which point its exact location becomes known.

2. Many-Worlds Interpretation

This interpretation suggests that all possible outcomes of a wave function exist in separate parallel universes.

Example:
In the double-slit experiment, the particle passes through both slits in separate universes, with each outcome realized in its own branch.

—

Conclusion

The wave function is a cornerstone of quantum mechanics, providing a mathematical framework to describe the probabilistic nature of particles and systems at microscopic scales. From predicting the behavior of electrons in atoms to enabling technologies like quantum computers, the wave function has reshaped our understanding of reality. Despite ongoing debates about its interpretation, its applications and insights continue to drive advancements in science and technology.