An elastic collision is a type of collision where the total kinetic energy and total momentum of the system are conserved. In such collisions, the colliding objects rebound without any permanent deformation, generation of heat, or energy loss to sound or other forms of energy. Elastic collisions are idealized events that occur most commonly in physics problems, molecular interactions, and certain real-world scenarios like collisions between gas molecules.

The study of elastic collisions is central to understanding how objects interact in environments where energy conservation is significant. This article explores the principles, equations, and examples of elastic collisions to provide a comprehensive understanding of this fundamental concept.
—
Characteristics of an Elastic Collision
Elastic collisions are characterized by the following key properties:
1. Conservation of Momentum: The total momentum of the system before and after the collision remains constant.
![]()
2. Conservation of Kinetic Energy: The total kinetic energy of the system is conserved before and after the collision.
![]()
3. Elastic Rebound: The objects separate after collision with no lasting deformation or energy loss.
—
Equations Governing Elastic Collisions
For a one-dimensional elastic collision involving two objects with masses ![]() and
and ![]() , the final velocities (
, the final velocities (![]() and
and ![]() ) are determined by the following equations:
) are determined by the following equations:
![]()
![]()
Where:
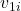 and
and 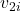 : Initial velocities of the two objects.
: Initial velocities of the two objects.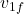 and
and 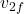 : Final velocities of the two objects.
: Final velocities of the two objects.
These equations ensure that both momentum and kinetic energy are conserved.
—
Examples of Elastic Collisions
1. Collision of Two Identical Balls
Consider two identical balls, each with mass ![]() , moving in a straight line. The first ball (
, moving in a straight line. The first ball (![]() ) moves with velocity
) moves with velocity ![]() , while the second ball (
, while the second ball (![]() ) is stationary (
) is stationary (![]() ).
).
Using the equations for ![]() and
and ![]() :
:
![]()
![]()
After the collision, the first ball stops, and the second ball moves with the initial velocity of the first ball. This is a typical example of a perfect elastic collision.
—
2. Billiard Balls on a Table
Billiard balls are a real-world approximation of elastic collisions, as they rebound off each other with minimal energy loss. For instance, if a moving ball strikes a stationary ball head-on, it transfers most of its momentum and kinetic energy to the second ball.
—
3. Molecular Collisions
At the atomic level, gas molecules undergo elastic collisions with each other. These collisions are critical to maintaining the temperature and pressure of gases, as described by the kinetic theory of gases.
Example:
In an ideal gas, when two nitrogen molecules collide elastically, they exchange energy and momentum without losing kinetic energy to heat.
—
Conservation Laws in Elastic Collisions
1. Conservation of Momentum
The momentum of a system is the product of its mass and velocity. Elastic collisions conserve momentum, ensuring that the total momentum before and after the collision remains the same.
Example:
Two hockey pucks of masses ![]() each collide elastically. If puck
each collide elastically. If puck ![]() has an initial velocity of
has an initial velocity of ![]() and puck
and puck ![]() is stationary:
is stationary:
![]()
![]()
Solving for ![]() and
and ![]() , we find the velocities after the collision.
, we find the velocities after the collision.
—
2. Conservation of Kinetic Energy
Kinetic energy is conserved in elastic collisions, ensuring no energy is lost to sound, heat, or deformation.
Example:
If a ball of ![]() moving at
moving at ![]() collides elastically with a stationary
collides elastically with a stationary ![]() ball:
ball:
![]()
After the collision, the total kinetic energy remains ![]() , distributed between the two balls.
, distributed between the two balls.
—
Elastic Collisions in Two Dimensions
In two-dimensional collisions, the objects may scatter in different directions, but the principles of momentum and kinetic energy conservation still apply. The analysis involves resolving velocities into components along ![]() – and
– and ![]() -axes.
-axes.
Example:
Two hockey pucks collide on a frictionless surface. After the collision, their velocities and angles can be calculated by applying conservation laws separately to each axis.
—
Differences Between Elastic and Inelastic Collisions
| Property | Elastic Collision | Inelastic Collision |
|---|---|---|
| Kinetic Energy | Conserved | Not conserved; some energy is lost as heat or sound. |
| Momentum | Conserved | Conserved. |
| Post-Collision State | Objects rebound with no lasting deformation. | Objects may stick together or deform permanently. |
Example:
A rubber ball bouncing off the ground is nearly elastic, while a lump of clay hitting the ground is inelastic because it deforms and doesn’t rebound.
—
Real-World Applications of Elastic Collisions
1. Particle Physics
Elastic collisions are critical in particle accelerators, where subatomic particles collide to study fundamental interactions.
Example:
Protons in a collider undergo elastic collisions, transferring momentum and energy to probe the forces governing particle interactions.
2. Gas Dynamics
Elastic collisions between gas molecules determine macroscopic properties like pressure, temperature, and volume.
Example:
The ideal gas law, ![]() , relies on the assumption that gas molecules collide elastically.
, relies on the assumption that gas molecules collide elastically.
3. Sports
Many sports involve nearly elastic collisions, such as a basketball rebounding off the floor or a tennis ball hitting a racket.
Example:
The rebound height of a basketball depends on the elasticity of the collision with the floor.
—
Limitations of Perfect Elastic Collisions
While elastic collisions are a useful idealization, they are rare in real-world macroscopic systems due to energy losses to heat, sound, and deformation.
Example:
When two cars collide, the collision is highly inelastic because significant energy is lost to damage and sound.
—
Conclusion
Elastic collisions exemplify the elegance of conservation laws in physics, where momentum and kinetic energy remain unchanged. These collisions occur frequently in microscopic systems, like gas molecules and particle physics experiments, and provide a foundation for understanding broader physical phenomena. While perfect elastic collisions are rare in the macroscopic world, their principles offer valuable insights into energy transfer and interactions across a range of disciplines.