What Is Planck’s Constant? – en-www.sridianti.com

Planck’s constant, denoted by $h$ , is one of the most fundamental constants in physics, representing the quantization of energy at the smallest scales. Introduced by Max Planck in 1900, it serves as the cornerstone of quantum mechanics. Planck’s constant relates the energy of a photon to its frequency, illustrating that energy is not continuous but comes in discrete packets, or quanta.

The relationship is expressed as:

$E = h \nu$

Where:

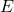$E$ : Energy of a photon (in joules, J)
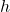$h$ : Planck’s constant ( $6.626 \times 10^{-34} \, \text{J·s}$ )
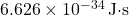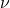$\nu$ : Frequency of the photon (in hertz, Hz)

Planck’s constant reveals the quantized nature of energy and is instrumental in describing phenomena at atomic and subatomic scales. This article delves into the significance of Planck’s constant, its role in quantum mechanics, and its applications, with examples illustrating its impact on modern physics.

—

Understanding Planck’s Constant

Planck’s constant bridges the realms of wave and particle physics by quantifying how energy interacts with electromagnetic waves. It defines the smallest possible unit of energy exchange, highlighting that energy is not infinitely divisible but exists in discrete amounts.

The Value of Planck’s Constant

The accepted value of Planck’s constant is:

$h = 6.626 \times 10^{-34} \, \text{J·s}$

Its small value reflects the incredibly minute scale of quantum phenomena, emphasizing why classical mechanics fails to explain atomic-scale interactions.

Example:
A photon of light with a frequency of $5 \times 10^{14} \, \text{Hz}$ has energy:

$E = h \nu = (6.626 \times 10^{-34}) \cdot (5 \times 10^{14}) = 3.313 \times 10^{-19} \, \text{J}.$

This energy is tiny on a macroscopic scale but significant in atomic interactions.

—

Historical Context: Max Planck’s Discovery

In 1900, Max Planck was studying blackbody radiation—how objects emit and absorb energy at different temperatures. Classical theories, like Rayleigh-Jeans law, predicted an “ultraviolet catastrophe,” where energy at high frequencies would diverge to infinity. This contradicted experimental observations.

Planck resolved this issue by proposing that energy is emitted in discrete packets, or quanta, proportional to the frequency of radiation. This groundbreaking idea introduced the concept of Planck’s constant and laid the foundation for quantum mechanics.

—

Applications of Planck’s Constant

Planck’s constant plays a pivotal role in various quantum phenomena and physical laws. Below are its key applications:

1. Energy of Photons

Planck’s constant directly relates the energy of photons to their frequency, providing insights into light’s particle-like behavior. This relationship is crucial in explaining phenomena like photoelectric effect and spectroscopy.

Example:
Ultraviolet light ( $\nu = 10^{15} \, \text{Hz}$ ) has more energetic photons than red light ( $\nu = 4 \times 10^{14} \, \text{Hz}$ ) due to the proportionality:

$E = h \nu.$

2. Planck-Einstein Relation

Albert Einstein expanded on Planck’s work to explain the photoelectric effect, showing how photons can eject electrons from a metal surface when their energy exceeds the material’s work function. This relation is:

$E = h \nu - \phi,$

where $\phi$ is the work function.

Example:
For a metal with $\phi = 2.5 \, \text{eV}$ , a photon with $\nu = 10^{15} \, \text{Hz}$ has energy:

$E = h \nu = (6.626 \times 10^{-34}) \cdot (10^{15}) = 6.626 \times 10^{-19} \, \text{J} \, \text{or} \, 4.14 \, \text{eV}.$

Since $E > \phi$ , the photon can eject an electron.

3. Quantum Mechanics and Wave-Particle Duality

Planck’s constant underpins wave-particle duality, a fundamental principle in quantum mechanics. It shows how particles, like electrons, exhibit wave-like properties.

De Broglie Wavelength:
Louis de Broglie used Planck’s constant to relate a particle’s momentum ( $p$ ) to its wavelength ( $\lambda$ ):

$\lambda = \frac{h}{p}.$

Example:
An electron with momentum $p = 9.1 \times 10^{-24} \, \text{kg·m/s}$ has a wavelength:

$\lambda = \frac{h}{p} = \frac{6.626 \times 10^{-34}}{9.1 \times 10^{-24}} \approx 7.28 \times 10^{-11} \, \text{m}.$

This wavelength is comparable to atomic dimensions, explaining electron diffraction.

—

Planck’s Constant and Heisenberg’s Uncertainty Principle

Planck’s constant is central to Heisenberg’s uncertainty principle, which states that certain pairs of physical properties, like position ( $x$ ) and momentum ( $p$ ), cannot be simultaneously measured with arbitrary precision:

$\Delta x \Delta p \geq \frac{\hbar}{2},$

where $\hbar = \frac{h}{2\pi}$ is the reduced Planck’s constant.

Example:
For an electron localized to within $\Delta x = 10^{-10} \, \text{m}$ , the uncertainty in momentum is:

$\Delta p \geq \frac{\hbar}{2 \Delta x} = \frac{6.626 \times 10^{-34} / (2\pi)}{2 \cdot 10^{-10}} \approx 5.27 \times 10^{-25} \, \text{kg·m/s}.$

This highlights the inherent limits of precision in quantum systems.

—

Planck Units and Fundamental Constants

Planck’s constant defines the Planck units, a system of natural units based on fundamental physical constants. These units provide a framework for understanding phenomena at the quantum scale.

Planck Energy

The energy scale defined by Planck’s constant is enormous:

$E_P = \sqrt{\frac{\hbar c^5}{G}},$

where $G$ is the gravitational constant and $c$ is the speed of light.

Planck Length and Time

Planck’s constant also defines the smallest meaningful length ( $l_P$ ) and time ( $t_P$ ) scales:

$l_P = \sqrt{\frac{\hbar G}{c^3}}, \quad t_P = \sqrt{\frac{\hbar G}{c^5}}.$

These units suggest a fundamental quantum-gravitational scale where classical physics breaks down.

—

Real-World Examples of Planck’s Constant

1. Spectroscopy

In spectroscopy, Planck’s constant is used to calculate the energy of photons emitted or absorbed by atoms during electronic transitions.

Example:
In hydrogen, the transition from $n=3$ to $n=2$ emits a photon with frequency $\nu = 4.57 \times 10^{14} \, \text{Hz}$ . The photon’s energy is:

$E = h \nu = (6.626 \times 10^{-34}) \cdot (4.57 \times 10^{14}) = 3.03 \times 10^{-19} \, \text{J}.$

2. LEDs and Semiconductors

The efficiency of light-emitting diodes (LEDs) and semiconductors is evaluated using Planck’s relation, linking photon energy to the bandgap of the material.

Example:
A red LED emits light with $\nu = 4.3 \times 10^{14} \, \text{Hz}$ . The photon energy is:

$E = h \nu = 2.85 \times 10^{-19} \, \text{J}.$

3. Atomic Clocks

Planck’s constant determines the precision of atomic clocks, which rely on the quantized energy levels of cesium atoms.

Example:
The frequency of cesium-133’s atomic transition ( $\nu = 9.19 \times 10^9 \, \text{Hz}$ ) is used to define the second in the SI system.

—

The Redefinition of the Kilogram

In 2019, Planck’s constant became the basis for redefining the kilogram in the International System of Units (SI). The kilogram is now defined using a fixed value of Planck’s constant, replacing the historical reliance on a physical artifact.

This redefinition ties the kilogram to fundamental constants, enhancing the precision and universality of measurements.

—

Conclusion

Planck’s constant is a cornerstone of quantum mechanics, embodying the quantization of energy and defining the scale of quantum phenomena.